데이터 분석/데이터 사이언스
데이터 사이언스 - 5. 기초 통계 및 확률 (5.2 확률 및 확률분포)
개발_노트
2025. 3. 20. 16:01
5.2 확률 및 확률분포
확률 및 확률분포는 데이터 분석과 머신러닝의 핵심 개념으로, 데이터가 어떻게 분포하는지, 특정 값이 나타날 확률이 얼마나 되는지를 설명하는 데 사용된다.
이 장에서는 확률 변수(Probability Variable), 확률 밀도 함수(Probability Density Function, PDF), 그리고 주요 확률분포(정규분포, 이항분포, 포아송 분포)를 다룬다.
5.2.1 확률과 확률 변수
✅ 확률(Probability)
- 어떤 사건(Event)이 발생할 가능성을 나타내는 값
- 0(절대 발생하지 않음) ~ 1(반드시 발생) 사이의 값을 가짐
✅ 확률 변수(Probability Variable, Random Variable)
- 확률에 의해 결정되는 변수
- 특정 값이 발생할 확률이 있음
- 이산형(Discrete)과 연속형(Continuous)으로 구분됨
① 이산형 확률 변수 (Discrete Random Variable)
- 특정한 값만 가질 수 있는 확률 변수
- 예) 주사위를 던졌을 때 나오는 숫자 {1, 2, 3, 4, 5, 6}
- 이항분포, 포아송 분포 등이 포함됨
② 연속형 확률 변수 (Continuous Random Variable)
- 특정 구간 내에서 무한한 값을 가질 수 있는 확률 변수
- 예) 사람의 키, 몸무게, 온도 등
- 정규분포, 균등분포 등이 포함됨
5.2.2 확률 밀도 함수 (Probability Density Function, PDF)
✅ 확률 밀도 함수(PDF, Probability Density Function)
- 연속 확률 변수가 특정 값 근처에서 나타날 가능성을 나타내는 함수
- X축: 데이터 값, Y축: 확률 밀도
- 면적이 1이 되도록 정규화됨
예를 들어, 정규분포의 확률 밀도 함수(PDF)는 다음과 같다:

📌 확률 밀도 함수(PDF) 시각화 예제
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
# 정규분포의 확률 밀도 함수 시각화
x = np.linspace(-4, 4, 100)
y = stats.norm.pdf(x, loc=0, scale=1) # 평균 0, 표준편차 1
plt.plot(x, y, color="blue", label="Normal Distribution PDF")
plt.xlabel("X")
plt.ylabel("Probability Density")
plt.title("Probability Density Function (PDF)")
plt.legend()
plt.show()
✅ 해석
- 곡선 아래의 면적 합이 1
- 평균을 중심으로 대칭적인 정규분포 곡선
5.2.3 주요 확률 분포
확률 분포는 확률 변수가 특정 값들을 가질 확률을 나타내는 분포이다.
이 장에서는 정규분포, 이항분포, 포아송 분포를 설명한다.
① 정규분포 (Normal Distribution, Gaussian Distribution)
✅ 정규분포란?
- 데이터가 평균을 중심으로 대칭적으로 분포하는 확률 분포
- 자연현상에서 많이 관찰됨 (예: 키, 몸무게, 시험 점수)
✅ 정규분포의 특징
- 평균을 중심으로 좌우 대칭
- 68-95-99.7 법칙 적용
- 평균 ±1표준편차 → 68%의 데이터 포함
- 평균 ±2표준편차 → 95%의 데이터 포함
- 평균 ±3표준편차 → 99.7%의 데이터 포함
📌 정규분포 시각화 예제
# 정규분포 시각화
x = np.linspace(-4, 4, 100)
y = stats.norm.pdf(x, loc=0, scale=1)
plt.plot(x, y, color="blue", label="Normal Distribution")
plt.fill_between(x, y, alpha=0.2) # 곡선 아래 영역 강조
plt.xlabel("X")
plt.ylabel("Probability Density")
plt.title("Normal Distribution")
plt.legend()
plt.show()
✅ 정규분포의 활용 예시
- 머신러닝 모델의 가정 (예: 선형 회귀)
- 신호 처리, 금융 분석, 자연과학
② 이항분포 (Binomial Distribution)
✅ 이항분포란?
- 성공/실패처럼 두 가지 결과만 존재하는 실험을 여러 번 반복했을 때의 확률 분포
- 예) 동전을 10번 던졌을 때, 앞면이 나오는 횟수 분포
✅ 이항분포 공식
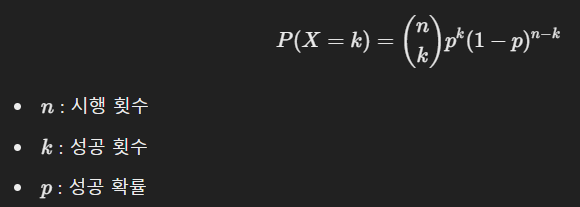
📌 이항분포 시각화 예제
# 이항분포 시각화
n, p = 10, 0.5 # 시행 횟수 10, 성공 확률 0.5
x = np.arange(0, n+1)
y = stats.binom.pmf(x, n, p)
plt.bar(x, y, color="green", alpha=0.7)
plt.xlabel("Successes (k)")
plt.ylabel("Probability")
plt.title("Binomial Distribution (n=10, p=0.5)")
plt.show()
✅ 이항분포 활용 예시
- 동전 던지기 실험
- A/B 테스트 결과 분석
③ 포아송 분포 (Poisson Distribution)
✅ 포아송 분포란?
- 일정한 시간 또는 공간에서 사건이 발생하는 횟수를 나타내는 확률 분포
- 예) 1시간 동안 도착하는 고객 수, 웹사이트에 접속하는 사용자 수
✅ 포아송 분포 공식

📌 포아송 분포 시각화 예제
# 포아송 분포 시각화
λ = 5 # 평균 발생 횟수
x = np.arange(0, 15)
y = stats.poisson.pmf(x, λ)
plt.bar(x, y, color="red", alpha=0.7)
plt.xlabel("Occurrences (k)")
plt.ylabel("Probability")
plt.title("Poisson Distribution (λ=5)")
plt.show()
✅ 포아송 분포 활용 예시
- 콜센터에 걸려오는 전화 수
- 서버에 접속하는 사용자 수
결론
확률 및 확률분포는 데이터의 패턴을 이해하고 예측하는 데 필수적인 개념이다.
- 정규분포 → 평균을 중심으로 대칭적으로 분포
- 이항분포 → 성공/실패 실험의 반복적인 시행 결과
- 포아송 분포 → 일정한 시간/공간에서 사건 발생 횟수
이러한 확률분포 개념을 이해하면 데이터 분석, 통계 모델링, 머신러닝에서 더 깊이 있는 분석이 가능해진다.